Math...

Just the word causes irritation and stress. There’s even a name for it: Math anxiety. Carrying, borrowing, long division, finding the common denominator, solving for x,…all of these procedures that had to be memorized! And it wasn’t forgiving either. A single mistaken step anywhere in the problem always (always) gave you the wrong answer. It’s not surprising, then, that most grew to view math as a necessary evil- magical incantations that might as well have been in Latin;repetitive and incomprehensible rites invoking the spirits for answers to questions, many times questions nobody really cared all that much about.

But when one looks past all the procedures and steps to very the core, to the heart of it, there is a deep magic to mathematics that can be observed. In many ways, mathematicians have been explorers and artists in a landscape that exists completely in the mind. And yet that mental landscape has, time and again, given us the tools to truly understand and manipulate the world around us.

Consider how numbers were discovered/invented. We can imagine some enterprising shepherd trying to keep track of how large his flock is. Or maybe a fisherman has caught some fish and wants to know if he has enough for his family. Thus, you have the natural numbers: 1, 2, 3, 4, 5 and so on. (And interestingly enough, some cultures didn’t even go that far, but instead counted this way: 1, 2, many. After 2 it’s all just a lot of numbers :). You can still figure out if you have enough fish for everyone, though, by simply pairing one fish to each person. If you run out of fish before you run out of people, you don’t have enough.) But let’s say that one of your sheep foals a lamb. Now you have to begin adding. Or let’s say you kill one of you sheep for food. Now you have to subtract. Those are natural arithmetic operations that arise almost instantly out of the natural numbers.

But let’s say you have 2 sheep that each foal a lamb? Now, you have to add 1 twice. Thus, multiplication, or adding groups of objects, is born. Let’s use dogs instead so we can play with bigger numbers. You have 2 female dogs and they each have a litter of 6 puppies. So you have 2 groups of 6 puppies, which you manually add up to 12. Multiplication is merely a way of adding large groups of numbers. Pretty soon, however, it becomes efficient to know what the multiples of common numbers are so that you don’t have to actually add 5 new beads from 8 different vendors. Instead you just know 5 x 8 is 40.

Conversely, what if you decided to leave your flock of 40 to your 2 sons (or 5 sons, for that matter)? You needed to divide and thus, you have division. But notice that just as subtracting is the opposite of adding, dividing into groups (division) is the opposite of adding groups together (multiplication). These are merely opposite operations- one undoes the other. If I add 5 and then take away 5, I am left with the original number. If I take 4 groups of 5 and put them together and then break that back into 4 groups, I am left with a group of the original number.

But what if I had 5 sheep and sold 5 of them? How many would I have? None. But what is that? It’s nothing. Can ‘nothing’ be thought of as a number? This is where we first begin to see some of the magic of mathematical thought. Up until this time, numbers do not exist by themselves. We have 5 sheep, we have 2 cows and so on. They are 5 of something. They are adjectives, describing a noun. But once man took the leap and thought of numbers themselves as some-thing- as a noun- the world changed. Now, numbers could exist independently of the objects they were describing. 3 was one thing and 3 cows was another. A new world came into existence, the realm of numbers. And the first newly conceptualized denizen of that realm was “nothing”. We call it zero.

Together with the natural numbers 1-9, zero is what eventually freed us from having to come up with symbols for each number. Some peoples, like the Greeks and Hebrews assigned a number to each letter. Even the Roman’s did that, with letters that doubled as numerals: I (1), V (5), X (10), L (50), C (100), M (1000), and so on. But what if you wanted to express larger and larger numbers? 2010 is MMX. 1992 is MCMXCII. Even worse than merely expressing numbers, however, was performing arithmetic operations on them. Try multiplying 2010 and 1992 using Roman numerals. Give up yet? But our base-10 (the digits 0-9) numbering system allowed us to represent any number (no matter how large or small), all thanks to zero. How? Each column in a number had a positional value based on 10: 1000, 100, 10, 1, for example. Look at the number ‘10’. It simply means 1 unit of tens and 0 units of ones. The ‘0’ in the ones column is what makes all the difference between “10” and “1”. Or “100”, or “10,000,000,000” for that matter. (Good explanation here.)

Moreover, these columns made possible by 0 allow us to do mathematical operations on each individual number, simplifying any mathematical operation. 23 x 7 is done this way: (3 x 7) + (20 x 7). Remember trying multiply MMXX and MCMXCII? Much easier to multiply 1992 x 2010. All those basic arithmetic operations- addition, subtraction, multiplication, and division- were made much easier thanks to zero.

Simple enough (and of course 0 does more than that.) But let’s step back from the details and look again at the numbers. Now that the numbers exist independently of the things they represent, new questions can be asked. Not just what is 5-5? What about 5-6? When numbers were tied to things- were describing physical objects- that kind of question made no kind of sense. If you have 5 sheep, you can’t give away 6 (though if you start thinking of debt in these terms, it becomes important to figure this out.) But as long as you looked at numbers as piles or collections of things, that kind of question really makes no sense.

But now that numbers are imagined objects that exist by themselves, we don’t have to conceive of them just as collections. Other metaphors could be used to describe numbers and arithmetic. Measuring was common enough, whether beams of wood for a house or for measuring out a plot of land. So looking at numbers as distances on a line made sense. You even have 0 being the starting point. The metaphor of the number-line thus comes into being. So adding 5 + 0 means taking 5 steps to the right of the 0. Taking away 5 (walking backwards 5) returns you to 0. 2 x 6 becomes traveling the distance of 6 twice (or the distance of 2 6 times depending on perspective.) Dividing 12 by 6 (or by 4) means cutting that distance into 2 (or 3) sections. All the arithmetic operations still work and are conceivable. And 5-6? Well, the number-line metaphor for numbers allows us to start at 5, go back 5 spaces to 0 and then back one more! After all, if the numbers can go to the right of 0, why not the left?

And with that metaphorical leap, negative numbers were born. The number-line burst forth, out in either direction, off into infinity. On this line, the same arithmetic rules apply. Addition and subtraction make sense. If you have 5+2-10, you can easily see that you start at 5, move 2 units to the right, then 10 units to the left, so that you land 3 units on the left side of 0, or -3. In fact, addition and subtraction now becomes the same thing. Subtraction is just addition where one of the numbers is negative. 5-3 becomes 5+(-3), where (+)5 tells you to start at 5, facing to the right and -3 tells you to walk backwards 3 units. Multiplication begins simply enough: 2 x -3 means start at 0 facing right and walk backwards 3 units twice, or 6 units to the left of 0 (and vice versa, with -2 x 3). Thus, negative times a positive will always be negative. The positive sign of one number tells you to start at 0 facing right (towards the positive side) and how many times to repeat the steps, and the negative sign tells you that you will be walking backwards, to the left of the number-line, a certain number of units. And since division is the opposite of multiplication, then those same rules apply. -4 / 2 means start at the -4 and divide the distance between -4 and 0 into 2 sections. The division will occur at -2.

But what happens when a negative is multiplied by a negative? Well, with the right metaphor already in place (facing a certain direction indicated by the first sign and then walking a certain number of steps a certain number of times backwards or forwards based on the second sign) this too is doable. -2 x -3 means start at 0 facing the negative side of the line. Then walk backwards 3 units, doing this 2 times. Thus, we are at 0 facing to the left and walking backwards, which will always keep us on the right side of 0, which is positive. Thus, negative times a negative is a positive.

Division of a negative by a negative is a little trickier, however. For example, -6 ÷ -2. In reality, the metaphor about walking and distances and lengths begins to get overly complicated. But at this point, that’s not necessarily a hindrance because remember, these numbers aren’t actually lengths or quantities or anything. The number line was simply a metaphor. They exist independently of the physical reality they initially described. In reality, these metaphors only give us a clue, a hint, as to the answer for any of this. They actually don’t constitute proof. It can be proven, using algebra, that a negative times a negative is a positive, for all negative numbers (here).

But we won’t go that far. Let’s just use our intuition to figure this out (which is how math is always done first.) Remember, for a moment, that division is the opposite of multiplication. Division is not simply asking how many times a group of numbers appears in a whole (how many 7’s are in 21, for example, which is 3). An equivalent, and more abstract question, divorced from groups and quantities and measurements, is this: what number multiplied by 7 is 21? It’s the same question, but one deals with concrete objects in the real world (groups of objects or distances from a starting point) and one exists purely in the mental realm of numbers that has been created, using the rules we have discovered. And that answer is easy. 7 x 3 =21 therefore 21 ÷ 7=3. Thus, since -2 x 3= -6, then -6 ÷ -2 = 3. See that? We don’t need to worry about walking forwards or backwards, or about facing different directions. The numbers follow rules that are easy to remember. And since division is the opposite of multiplication, we can use that fact to state an answer. Numbers live and act in a world that is completely consistent and logical, but one that is in the mind. (Unsurprisingly, negative numbers remained controversial even up into the 1700’s, since they required such a paradigm shift in how we view numbers.)

This kind of discovery/creation of numbers based on legitimate arithmetic operations (in the previous example, subtraction) can be repeated to make new discoveries. 4 ÷ 2 is obviously 2. But what about 5 ÷ 2? Obviously, it’s more than 2 and less than 3. It’s 2 and some fraction of whole number. See where this goes? A new kind of number has to be created, one that is a fraction of a number. Obviously, this has application in the real world (pies, for example.) It’s not like it doesn’t make sense. But how do we express this as a number? It is undeniable, for example, that you can cut a pie in half. But a half means there are 2 pieces and we are taking one of them. So we can write this as ½. Note that this is left as a ratio of 2 numbers: 1 out of 2. It’s written using the ‘-‘, which simply division (see the ‘÷’ symbol? The dot on the top and bottom represent the upper and lower numbers of the ratio.) Another way is to use a decimal point (“.”) to separate the whole numbers from the fractional ones. ½ also is 0.5 because the ratio can be divided (using long division) to give us the actual number (5 tenths of a whole, which is half of the whole).

With the introduction of writing fractions of numbers as ratios, it became possible to see that you could write any numbers in many different ways. 2 could also be written as 4/2 or as 8/4 or as 10/5. ½ could be written as 4/8 or 8/16, etc. Numbers became even more abstract things that had an infinite number of faces or disguises, but still had it’s own identity. Numbers were a concept, an idea that could be expressed any way it needed to. Need to multiply by 1? You could use 2/2 or 5/5 or 124445563/124445563. (This trick is actually used quite a bit once you start adding fractions with different lower numbers- called denominators.) It didn’t matter. It was all the same number, just in the form you needed it to be. This kind of discovery gave people the tools to solve all manner of legitimate problems. I have 5 acres of land and each crop needs a half an acre for growth. I will loan you money, but you need to pay me back 6 cents for every dollar I’ve loaned you. I will complete the work in half an hour and I am getting paid $8 and hour. Finance, engineering, astronomy (under the guise of astrology) all required this new number system that allowed for fractions of whole numbers, expressed as ratios of two numbers. Therefore it was called the rational number system. The rules of arithmetic were worked out, certain things disallowed (like dividing by 0- here’s why, by the way) and the system was complete.

Now stop and think about that for a moment. From the natural counting numbers, we have created a whole slew of new numbers- zero, negative numbers, fractional numbers- using simple arithmetic. Do these numbers exist? In a sense, yes, at least in their usefulness. But then again, no. I mean , how can you show me -2 cows? Only when it applied to concepts like debt or loss can you even begin to say that, and even then you can’t have an actual -2 cows. And realistically speaking, while I can envision ½ of a pie, what about 12/1232534698335363 of a pie? How would I cut a pie into 1232534698335363 pieces? Is there an actual physical object that can exist with that ratio? In fact, there’s a probable limit for how small (or large, for that matter) things can get. Many scientists believe this lower limit to be the Planck length: 1.61625281×10e(−35) meters, using scientific notation. That means nothing can exist (be measured) that is smaller than that. And yet we can always write a number that is even smaller, like 1.61625281×10e(−36). Clearly, then, numbers can describe things that have no existence in this world. Again, they are separate constructs existing in a mental realm.

Conversely, though, there are physical lengths that cannot be written using the rational numbering system (and can only be approximated- meaning as you write it down, you can get closer and closer to the actual value but can’t ever actually write the whole number.) One example is said to have been discovered by a Greek named Hippasus, who was a follower of the ancient Greek mathematician Pythogoras (he of the Pythagorean formula fame). Supposedly, the discovery of such a number sent Pythogoras (who believed in the sacredness and divinity of numbers) into such rage that he had Hippasus drowned. A part of mathematics we haven’t touched on (though obviously it was affected and motivated the discoveries and creations of many of the things we have talked about) is geometry: The study and measurement of shapes like circles, squares and triangles and their properties (highly useful when you’re laying out fields, walls, pyramids and buildings). Over time, it was discovered that shapes followed the same mathematical rules. The area a rectangle used up was always its length x width. The area of triangle was always ½ its base x height. The ratio of the circumference of a circle to its diameter was always the same, a mysterious number called pi (π- depicted here) and was a little more than 3.14, and was useful for calculating the area circle used. Gradually these shapes were explored and other relationships were noticed. In particular, angles became important, the way two lines intersect. After all, if you’re building a stable wall, you need to make sure it is as securely positioned as possible. This happens when the wall is built at an exact right angle to the floor, or 90 degrees, or turns of a circle (The Babylonians used a base 360 number system, so a full circle turn was called 360 degrees, a half circle was then 180 degrees and half of that was 90 degrees.)

Various properties of these right triangles were studied. One in particular discovery was profound. No matter the length or size of a triangle, if one of the angles was 90 degrees, a specific relationship always held true. (This relationship between numbers is called an equation.)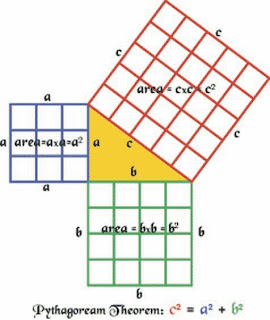 The relationship was this: a² + b² = c², where a and b are the lengths of the two legs that made the right angle and c is the line opposite the right angle. (a² means a x a and was called square because it’s actually the square created when both length and width of a rectangle are the same value a. See picture.) This was an astounding discovery. It is a property of triangles (the idea of triangles) that existed independently of any actual physical triangles. All right triangles obey this rule, whether it is a triangle whose sides are measured in miles or in inches. Practically speaking, this rule (the figuring out of what side lengths worked for it) allowed one to check quickly if something was at a right angle. For example, the numbers 3, 4, and 5 work for a,b, and c. Thus, you simply measure 3 feet, for example, going one direction, 4 across the ground in another direction, and then measure the distance from those end points. If it is 5, you have a right angle. If not, adjust the angle where the two legs (a and b) meet until the distance of c becomes 5, and you have made a right triangle.

Let’s create a right triangle whose legs (a and b) are both 1. That’s doable. The angles for the corners are now 45 degrees. So what is the length of c (called the hypotenuse)? If we take the Pythagorean formula a² + b² = c², we can plug in the numbers. 1² + 1² = c² so 2 = c². This means that c is a number that, when multiplied by itself, is 2. This kind of number is called a square root. For example, the square root of 4 is 2, since 4=2x2 or 2², and is written √4=2. So c= √2. What is this number? We can write out √4, √16, √64, √4/√16, etc, using the rational numbers, which would be 2, 3, 8, 2/4, etc. But what shocked the Pythagoreans was that it could be proved (here) that √2 could not be written out in anyway as a ratio of two numbers. Even the infinite decimals .3333….. or .6666….. (where the 3’s and 6’s extend off into infinity) could be written as a ratio: 1/3 and 2/3, respectively. But not √2. Nor could it be written out as a decimal, as decimal was just another way of writing ratios.

Now think about that for a minute. Here you have a length that you can see. If the triangle has legs that are the length of 1 inch, you can literally hold the length of c, the hypotenuse, of the triangle, in between your thumb and forefinger….and yet you can never write out what that distance is! It never repeats and it never stops. You just can’t do it! All you can ever do is choose some arbitrary point in the number and stop. (The first million digits of √2 are listed here) Since √2 can’t be written as a ratio of two numbers (which all numbers up to this point could be: 2, .33333…, 100, 1.5, etc, can all be written as, among other things, 2/1, 1/3, 1000/10, 3/2, etc) it was called an irrational number. This discovery was astounding (and, as can be seen by what supposedly happened to Hippasus, disturbing). You can’t ever write down the actual value of this number, even though it is real and it represents a real distance!

But even more amazing is the fact that it turns out most numbers are irrational. The √2 is just the tip of the iceberg. For example, the square root of any number that isn’t a perfect square is irrational. 4 is a perfect square: its root is 2. 9 is a perfect square: its root is 3. 16 is a perfect square: its root is 4. And so on. But all other square roots are irrational, that is, they cannot be written out completely or expressed as a fraction (or ratio). Pi (π) is also irrational, as is phi (φ-the golden ratio) as well as other numbers like e (called the banker’s constant for it’s use in calculating any kind of growth, which includes compound interest- nice article here).

It has been proven that there are more irrational numbers than rational numbers, on a number line. So if you were to select at random any number on the infinite number line, chances are you will hit an irrational number rather than rational. (Another way of saying this is that the infinity of rational numbers is much, much smaller than the infinity of irrational numbers. Mind-blowing, but a mathematical fact none-the-less. There are many “sizes” of infinity.)

So what do we call the whole number line (all the rationals and irrationals together), then? It is called the real number system. Further questions regarding other arithmetic operations led to the discovery of another kind of number: √-1 (which, when you think about it, makes no sense at first, either. After all, a negative times a negative is a positive, as is a positive times a positive. So what number times itself will be -1?) Eventually, this led to complex numbers being created, with a real component and an imaginary one using i, (i being the √-1. Nice explanation here )

Of course, more occurred than just the discovery or creation of new numbers. Mathematicians tried to apply their questioning and methods to everything. George Boole attempted to formulate logic and deduction into a consistent mathematical discipline. For example, if statement A is “The sky is blue” and statement B is “I am an alien” then the following deductions can be made. A OR B is true (since one of those statements is true). A AND B is false (since I am not, actually an alien.) NOT A (the opposite of A) is false. NOT B is true. You can work out algebraic rules and eventually prove things like: NOT (A OR B) = NOT (A) AND NOT (B). (In practice, you use symbols so that this would be written as: where + is “OR” and x is “AND” and the “-“ is NOT.) Others asked questions like whether the angles of a triangle drawn on a ball also add up to 180 degrees, like they do on a piece of paper. (They don’t.) Or whether there are different sizes of infinity (There are, which I mentioned above.) Can you add an infinite number of items (like1 + ½ + ¼ + 1/8 + 1/16 + ….) and get a finite number? (Yes. The answer for that sum is 2.) How can you tell without actually adding numbers forever? Can you write a formula for a geometric shape, like a circle? (Yes. r² = x² + y², where r is the radius and x and y are any real numbers that satisfy this equation. This formula is actually the Pythagorean theorem, where x and y are coordinates on a Cartesian plane.) Still others, like Isaac Newton and Gottfried Leibnitz, were forced to invent mathematical fields like calculus in order to better study the world around them (and calculus proved to be the foundation of whole new fields of mathematical study, provided new tools to explore previously discovered fields, as well as put them all on firm, proved foundations for the first time in history.)

Every time someone asked a question or branched out into a new region, it was if the vista opened up even wider. Soon, connections between areas were discovered, beautiful inter-relationships connecting them. Equations were discovered that linked disciplines together in beautiful ways and implied a subtle and breathtaking harmony to the world of numbers. One of the most famous, and considered by many as the most beautiful, is Euler’s identity: Somehow, this formula links the fields of geometry (π), complex number analysis (i), natural logarithms and calculus (e), basic arithmetic operations (addition and multiplication), the identity numbers 1 and 0 (which we talked about earlier) all together into a very simple and elegant formula. (More info about it can be found here and here).

But at this point, you may be wondering what all this is good for? Who cares? Well, for some people, the mental exercise, challenge and thrill of discovery is enough. And indeed, there is a beauty, symmetry and harmony to the whole thing, one with gems and truths that are astounding to discover and pleasing to understand. But aside from that, many of the maths that have been discovered or invented that originally were thought to be purely theoretical, have actually turned out to be tremendously useful and have practical application.

Just a few of examples illustrate this. Obviously, negative numbers found their usefulness in describing things like loss or debt (in balancing your checkbook, for instance), as well as in a host of sciences. In physics, particularly when designing moving machines, it proved powerful, once it was coupled with concepts like velocity. Velocity differs from speed from a physicist’s perspective. Speed is just that: distance per unit of time, as in miles per hour, meters per minute, etc. But there is no taking into account direction or changes in speed with that word. So velocity is defined as distance per unit of time in a particular direction, denoted by the sign (positive or negative). A velocity (v) of 4 miles per hour can be now be thought of as in a particular direction, west, for example. That would mean v= -4 mi/hr is 4 miles per hour going east. While that may seem dumb, it’s actually profoundly useful because now, equations of motion for things like falling objects or planes or rockets, can describe their behavior accurately. If you’ve got an equation showing the relationship for the upward velocity of rocket to the amount of force the engines generate and it shows the velocity becoming negative after a certain amount of time….well, that’s kind of a bad thing. You know your engines aren’t going to be strong enough to keep the rocket moving up and you better change something. (Good explanation here) Thus, what was initially just an abstract mental creation to answer questions like 4-7=? has proved tremendously useful. Our modern world, with its machinery, electronics, food production using chemical fertilizers and farm machinery and the like, and so on, would not exist had no one asked the question that required the invention of negative numbers.

Complex numbers (description here) have turned out to be tremendously useful when doing electrical engineering. The behavior of electrical currents can be described perfectly using complex numbers. Obviously, this would be critical when designing circuitry for everything from cell phones and computers to light switches and televisions. (Nice examples). Thus, even though the word “imaginary numbers” makes it seem made up and impractical, the mathematics is anything but.

Remember George Boole and his formulation of logic? Seems sort of useless doesn’t it? Who would actually use math to analyze what people said or wrote in order to see if it was true or false? Well, yet again, this Boolean Logic found a very practical application. You’re sitting in front of a computer right now, probably with a cell phone on your hip or desk. The digital circuitry (as opposed to the electrical circuitry mentioned above) of microchips in these things is described using Boolean logic, but instead of “true” and “false”, circuits use “on” and “off” or “1” and “0”. Designers literally build transistors that will perform logical operations like ANDing things together. We know that A AND B will be true only if both are true. Logically, that makes sense. The statement: “I am a man” AND “I am alive” is true only if both of those are true. So an AND-gate will take in two inputs and output the logical ANDing of them together. So if A=1 and B=1 then the output will be 1, otherwise the output is 0. NOT-gates reverse whatever was put in, so NOT A is 1 when A=0 and 0 when A=1. And so on. So designers will string AND, OR, and NOT-gates (as well as others) together in ways to produce circuits that do things. And these things are described perfectly by Boolean logic. A circuit that will add 2 numbers is shown below. It has the inputs for 2 numbers (A and B) and then outputs, Sum and the Carried digit. (To understand this, think about adding 19+3. You add the digits in the ones column, 9+3 to get the Sum of 12 and then Carry the 1 over into the tens column, so that you have 1(0)+1(0)=20, making a total of 22. This works the same way, only the numbers are converted to binary (base-2) format.) The equations describing both of these outputs are: S=A XOR B. C=A AND B. And you can string these components together repeatedly to create adders that handle any number of digits. And since multiplication is repeated addition, you can use the same circuit for that, with a few additional components to handle the repeated addition a certain number of times. A special form of subtraction can also be done using an adder, and thus, so can division. And so we have a rudimentary calculator. Obviously, circuits can get more and more complicated, so using Boolean algebra becomes critical in designing these systems. You work out exactly what inputs should generate what outputs, write that out as an Boolean equation, simplify the equation (much as you would in regular algebra), and then quite literally build the circuit using the equation, adding an AND-gate here, an OR-gate there, and so on. (More info here) And thus, our computer is born from mathematics that seemed useless.

The question concerning the angles of a triangle on a globe adding up to 180 degrees led into the strange realm of topology. Up until this was asked, the only geometry we had (and thought existed) was what worked on flat surfaces. And when you add the angles up in the interior of a triangle it is always 180 degrees (the drawing to the right kind of helps you see why.) But when you draw a triangle on a globe something different happens. (See below) Note the legs of the triangle and how they meet. Drawn on a piece of paper, they look curved, but in actuality they are straight lines. And the angles in this triangle are all 90 degrees, making the total 270 degrees! And this isn’t the only difference between the geometry of a flat surface and that of a sphere. The value of π (pi) can change too! So geometry is different depending on the shape of the surface, from a donut (called a torus) to a saddle (hyperbolic sphere), and these geometries can be worked out to be completely self contained and consistent and just as “true” as the geometry of flat surfaces. So what’s the point of these discoveries? Obviously, map making (projecting the image of our globe onto a flat surface) benefited from this. But one person in particular took the mathematics for this “rubber sheet geometry” and changed the world with it: Albert Einstein. When he began formulating his general theory of relativity, the mathematics he needed to describe his ideas about space and time had already been developed, as an abstract mental exercise, by Bernard Riemann in the previous century. It proved to be just the tool needed to express his ideas fully and allowed him to make predictions that, when tested, proved his theory was correct. Today, whenever you use GPS, or anything involving communication to satellites in orbit, the general theory of relativity must be factored in, and the mathematics that allowed for it was this “rubber sheet” (or non-Euclidean) geometry developed earlier as merely another mathematical exploration. (Account here and here). And this kind of thing- abstract math suddenly becoming useful in new sciences- goes on and on.

So that’s it. When I set out to write this, I didn’t intend for it to be this long or detailed, but the more I wrote, the more I wanted to say. Ultimately, I hope that this at least can help you to see how amazing mathematics can be. Most of us will probably never understand all of this, at least any time soon, nor was that my goal (and the truth is, nobody fully understands all of it.) Instead, I wanted to share some of the adventure of mathematical discovery, convey some of the beauty and elegance of mathematical insights, and dispel some of the fear and loathing of mathematics. My honest opinion is this: nothing prevents us from experiencing any of these discoveries and their beauty more than our negative attitude towards math. Bad teachers, poor explanations, and repetitious procedures can often create in us such a dislike for mathematics that we never go any further than the basics (and even hate doing that.) Conversely, at least in my experience, seeing the beauty and discovery of mathematical application and history can help one to overcome their dislike of (or, in my own case, failures in) math and even begin to delve deeper into the subject with the adventurous spirit in which it was created. And in the process, we can come to the same discoveries and experience the thrill of grasping many of these subtle relations for ourselves.

Math is such a strange thing. From simple counting and adding, an entire ‘world’ has been discovered, one that exists completely in the mind. And yet we can all ‘walk’ and ‘explore’ that world, discovering ‘valleys’ and ‘tunnels’, ‘mountains’ and ‘seas,’ as well as artistically and elegantly represent these beautiful structures. And most amazing of all is how, time and again, “islands” and “continents” in this imaginary world have helped us in the real world. Indeed, many aspects of our modern life exist only because of the tools and insights offered by that imaginary world. Many mathematical philosophers have expressed a profound sense of awe at the power of mathematics to help us understand the world. They are genuinely surprised at how effective and powerful it has been, how fortuitous it is that we tiny humans are actually able to come to comprehend how the universe works, using these tools. Mathematics itself appears to describe our universe beautifully. Regions of mathematics that still seem to have no practical application may yet be used as lights to illuminate even more of our world.

The famous astronomer Galileo made this observation, whose truth becomes clearer and clearer each year: "Mathematics is the language with which God has written the universe."